Image Filters

Note

The image processing test images can be downloaded from this website:

Image Processing Repository http://links.uwaterloo.ca/Repository.html

Image Smoothing and Edge Detection

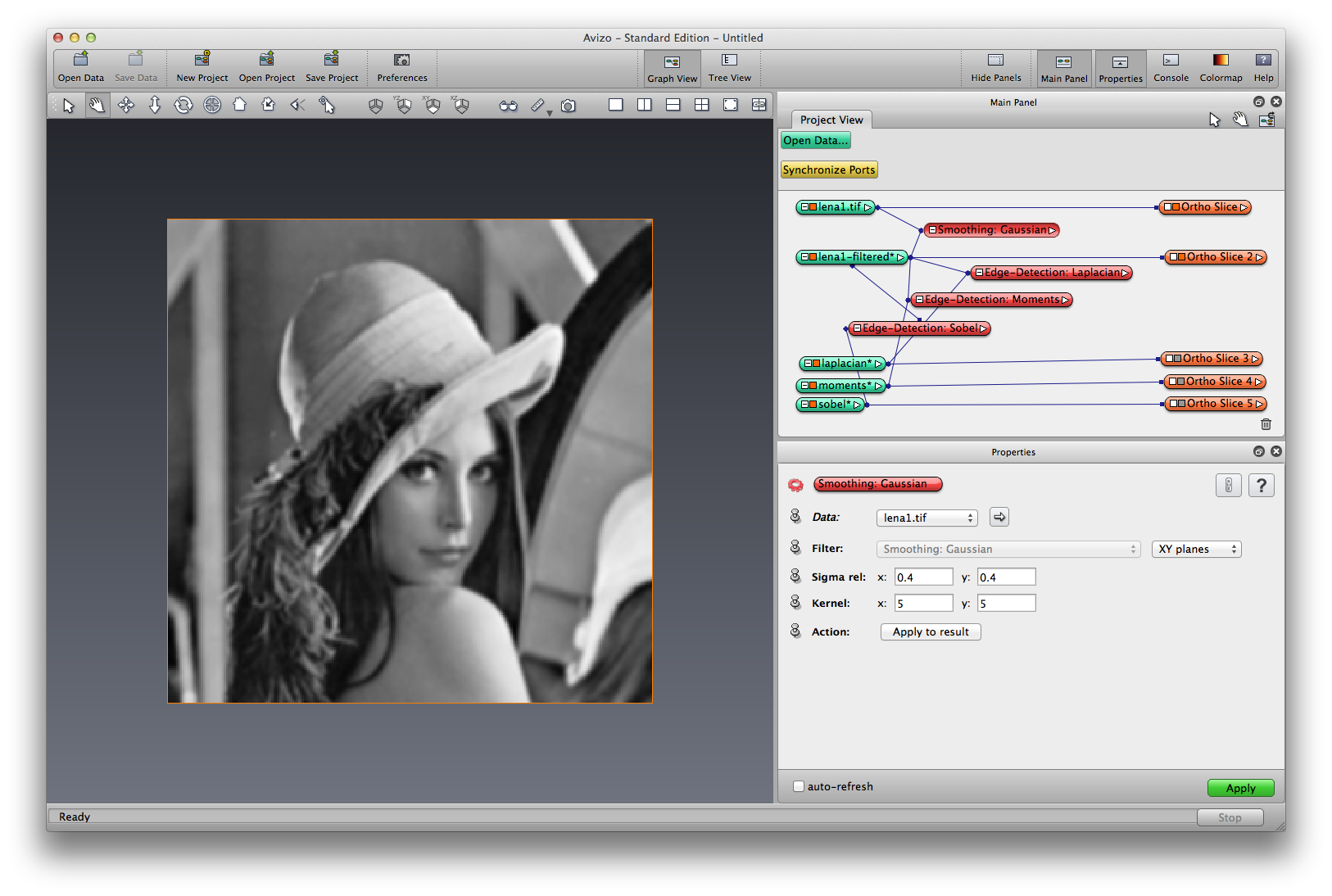
1. Lauch Avizo 7, open image lena.tif. Use orthoslice to visualize.

2. Right click on lena, choose Image Filters->Smoothing:Guassian, apply, a filtered image object is created, rename it lena-guassian. The Gaussian smoothing operator is a 2-D convolution operator that is used to smooth images and remove detail and noise. It uses a convolution kernel that represents the shape of a Gaussian (bell-shaped) hump.

   

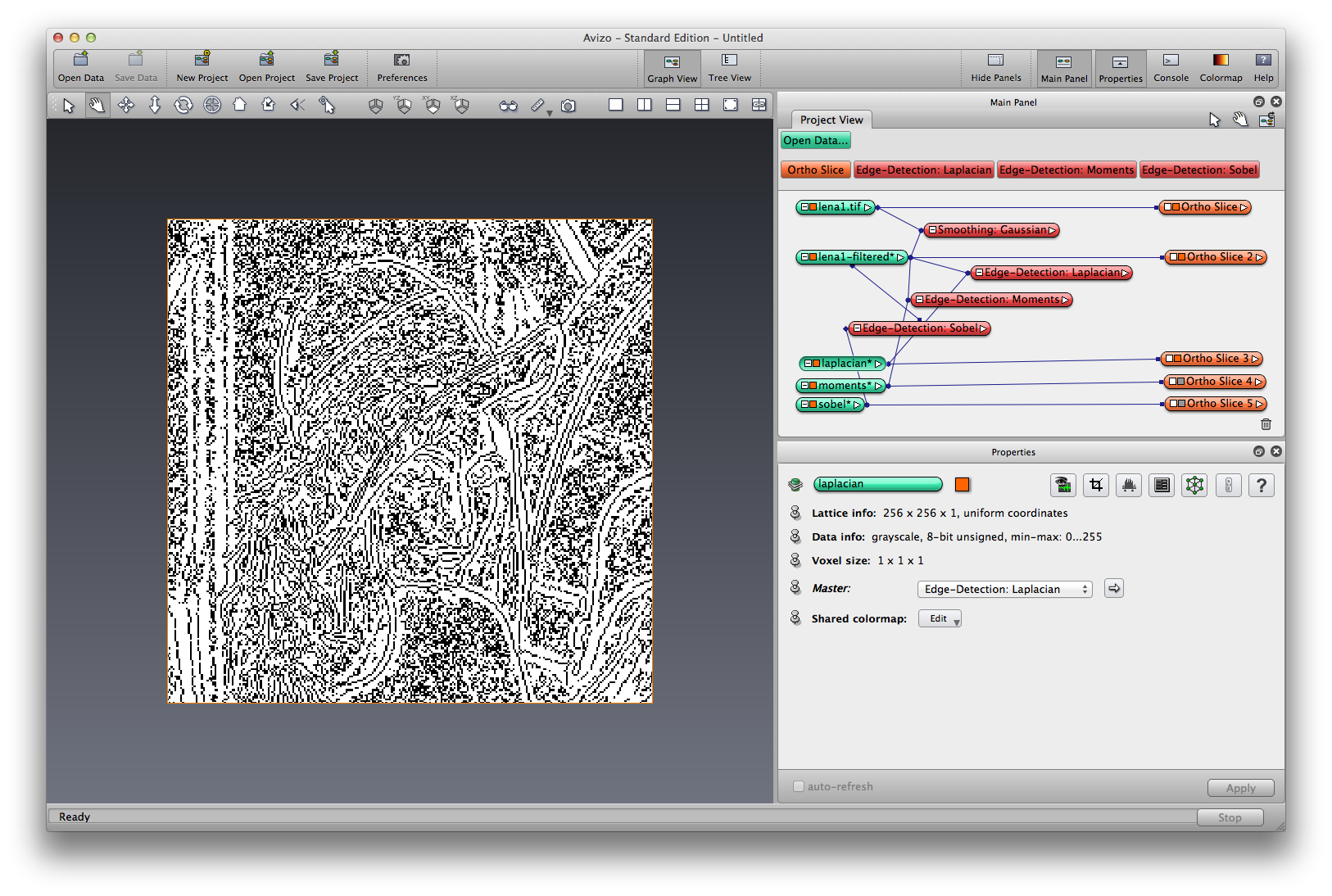
3. Let’s try some edge detection filters on the guassian filtered image. Right click on lena-guassian, choose Image Filters->Edge-Detection:Laplacian, apply, a filtered image is created. The Laplacian is a 2-D isotropic measure of the 2nd spatial derivative of an image.

   

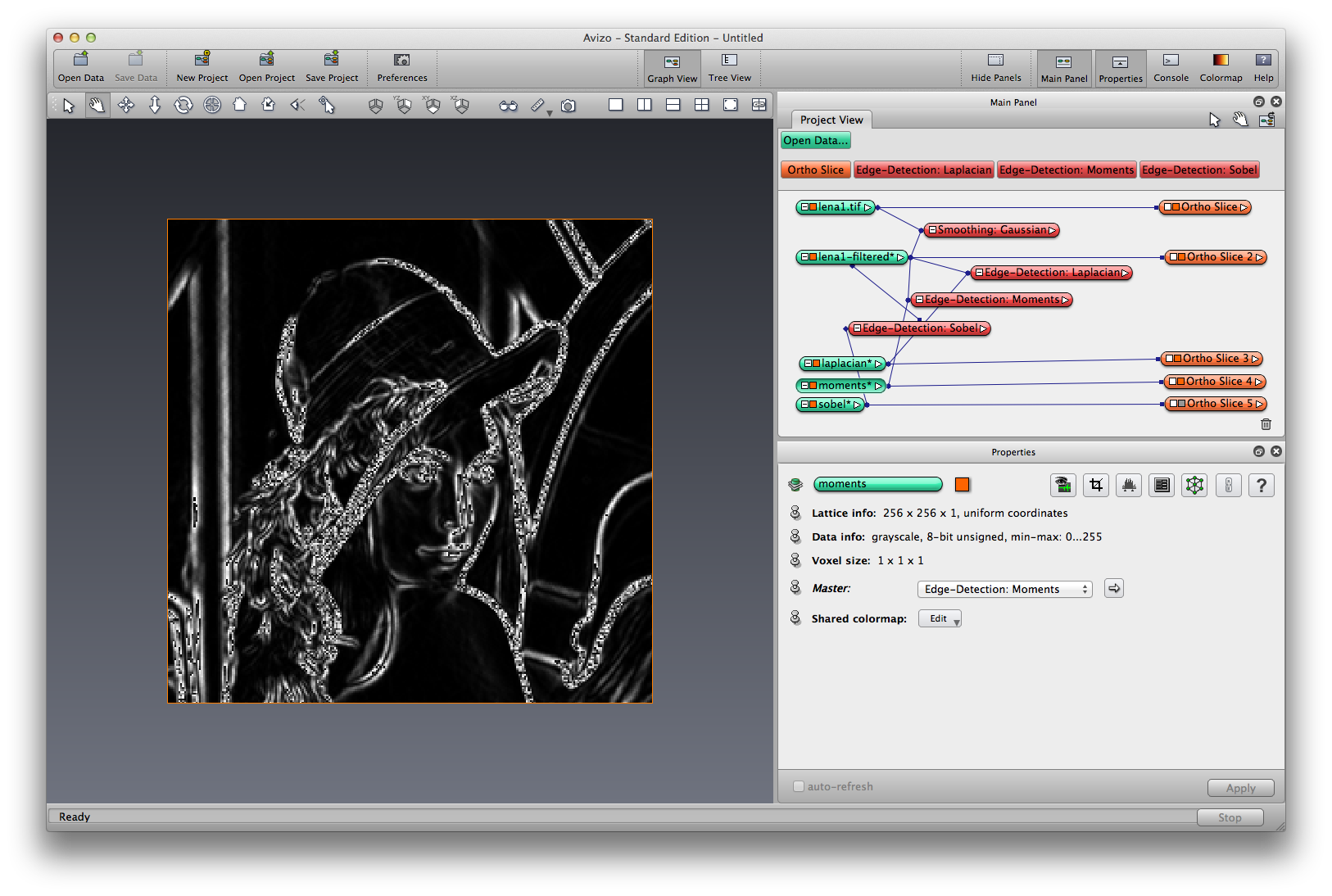
4. Right click on lena-guassian, choose Image Filters->Edge-Detection:Moments, apply, a filtered image is created. An image moment is a certain particular weighted average (moment) of the image pixels’ intensities. There are many types of image moments that are used to compute certain properties of an image. For example, a set of orthogonal complex moments of the image known as Zernike moments can be used to detect step edges with subpixel accuracy.

   

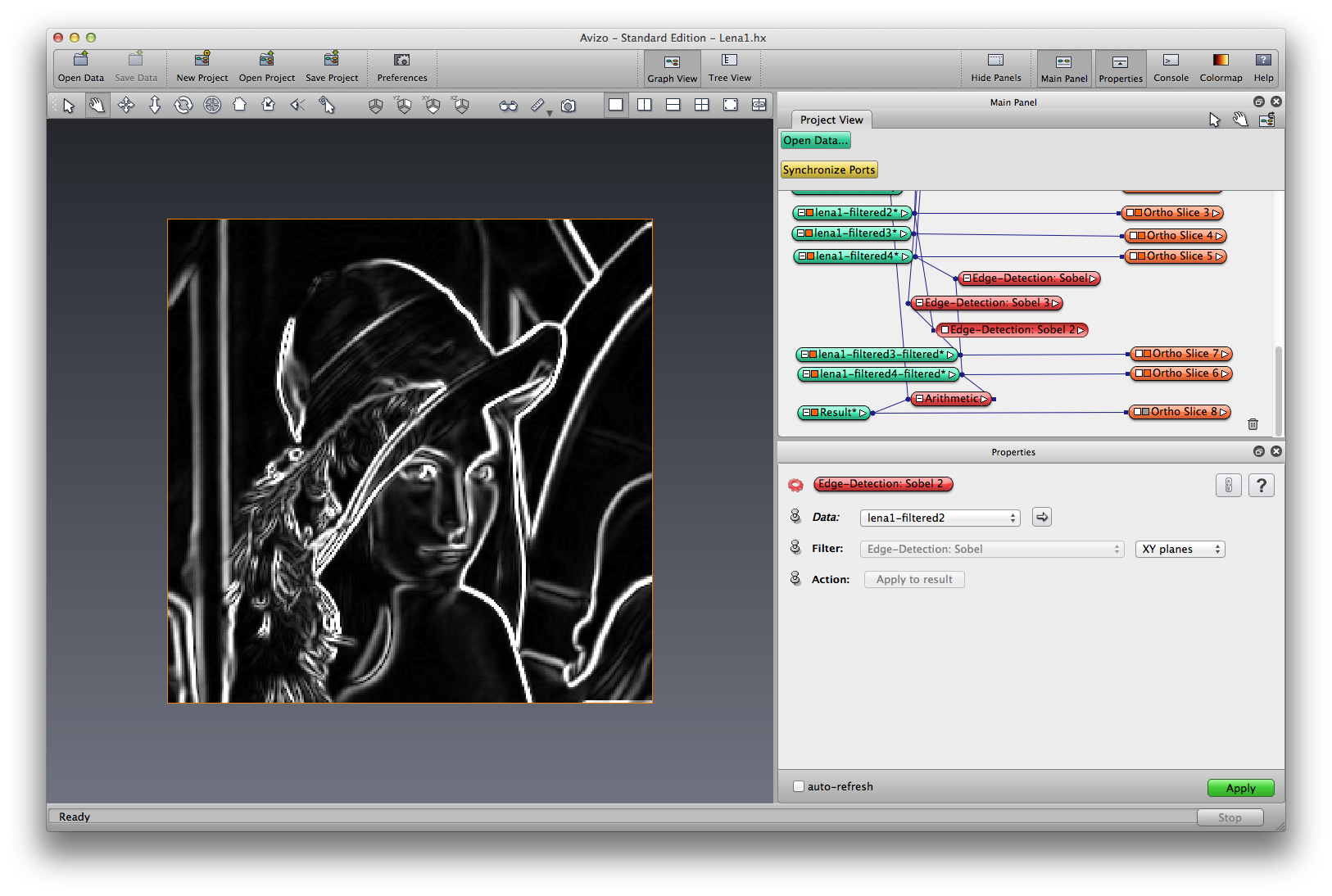
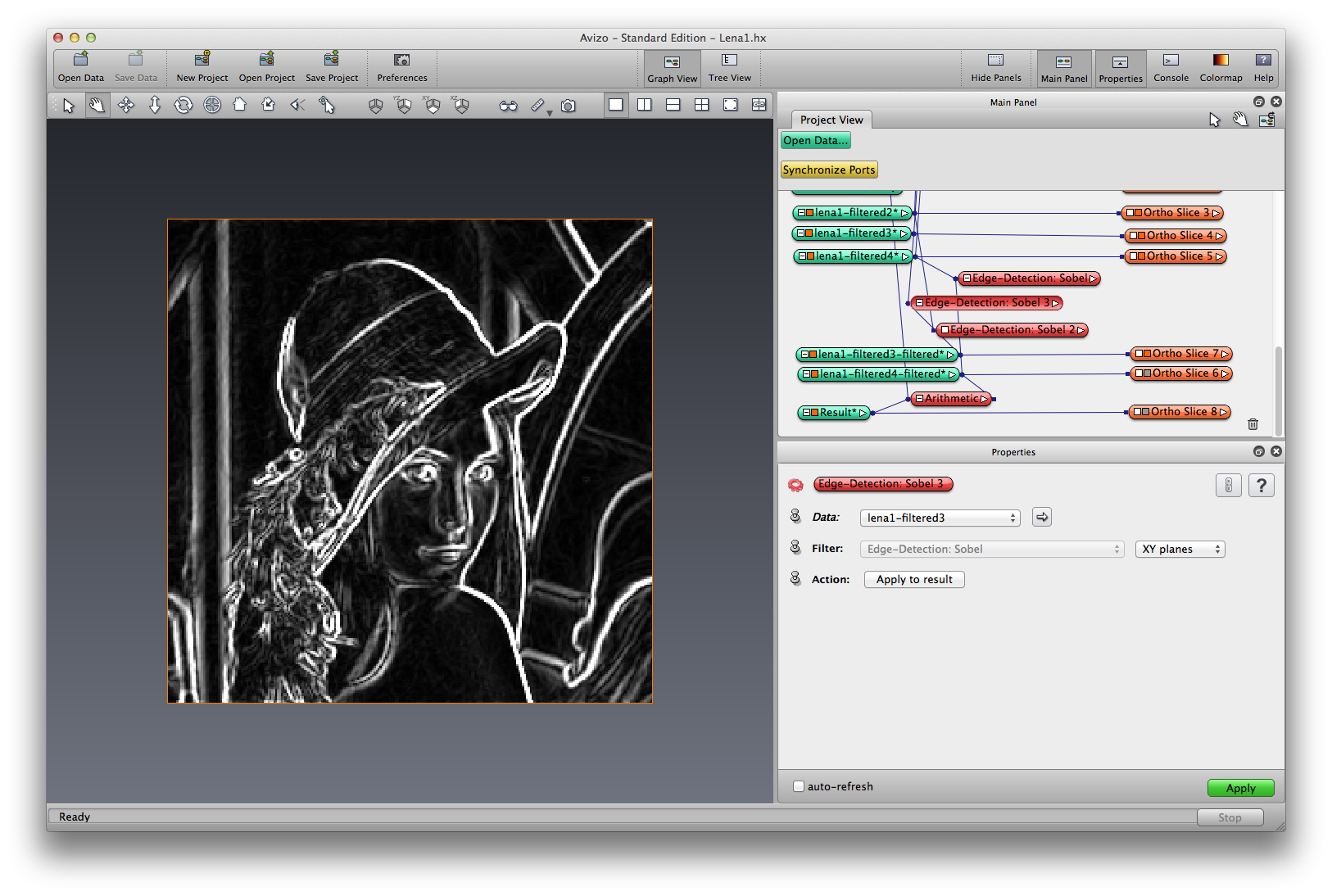
5. Right click on lena-guassian, choose Image Filters->Edge-Detection:Sobel, apply, a filtered image is created. The sobel operator uses two 3×3 kernels which are convolved with the original image to calculate approximations of the derivatives - one for horizontal changes, and one for vertical. The horizonal and vertical gradients are then used to compute the gradient magnitude.

   

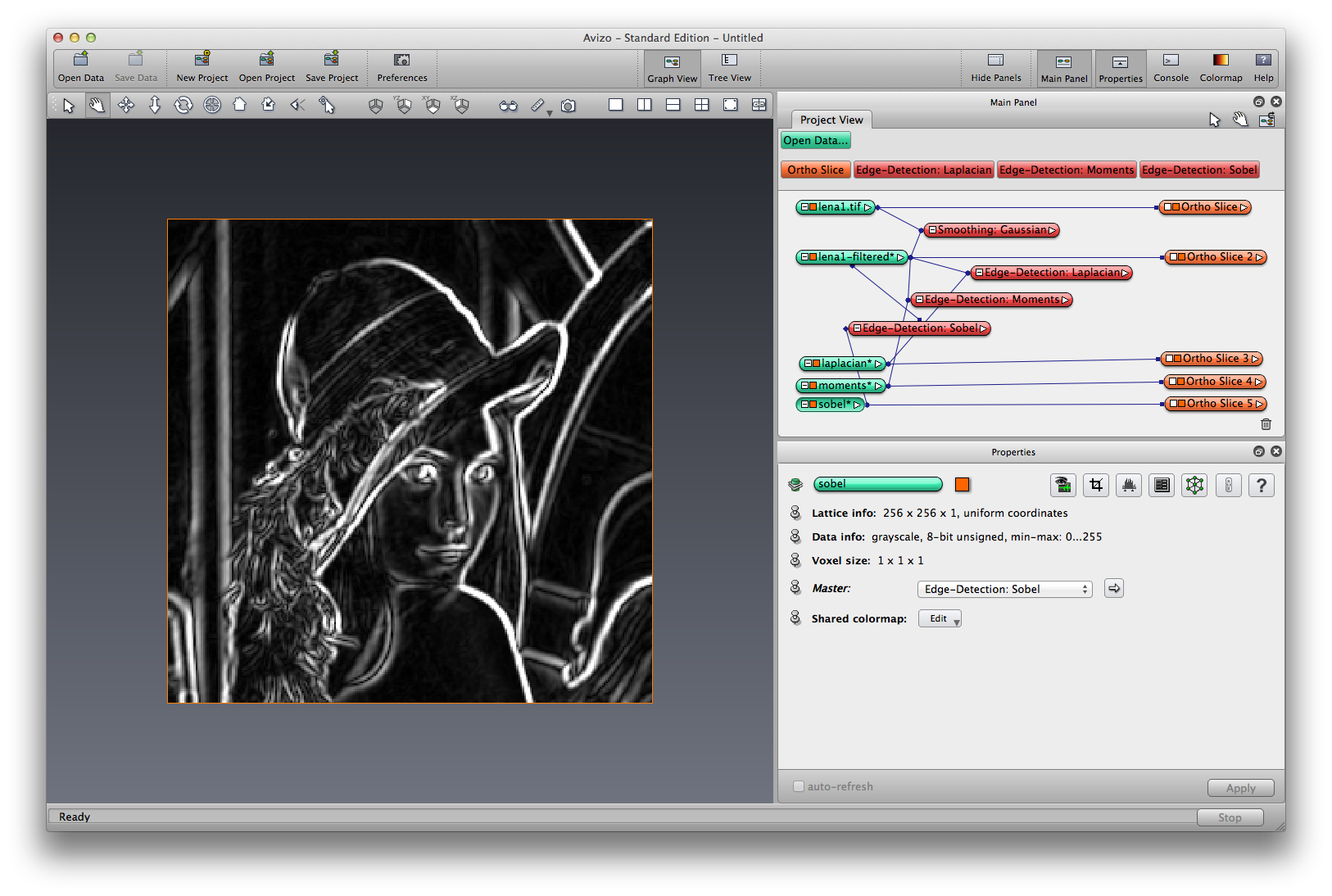
6. Now, let’s try some different smoothing filters other than guassian. Right click on lena, choose Image Filters->Smoothing:Anisotropic Diffusion, apply, a filtered image object is created, rename it lena-anisotropic. Anisotropic diffusion can be used to remove noise from digital images without blurring edges.

   

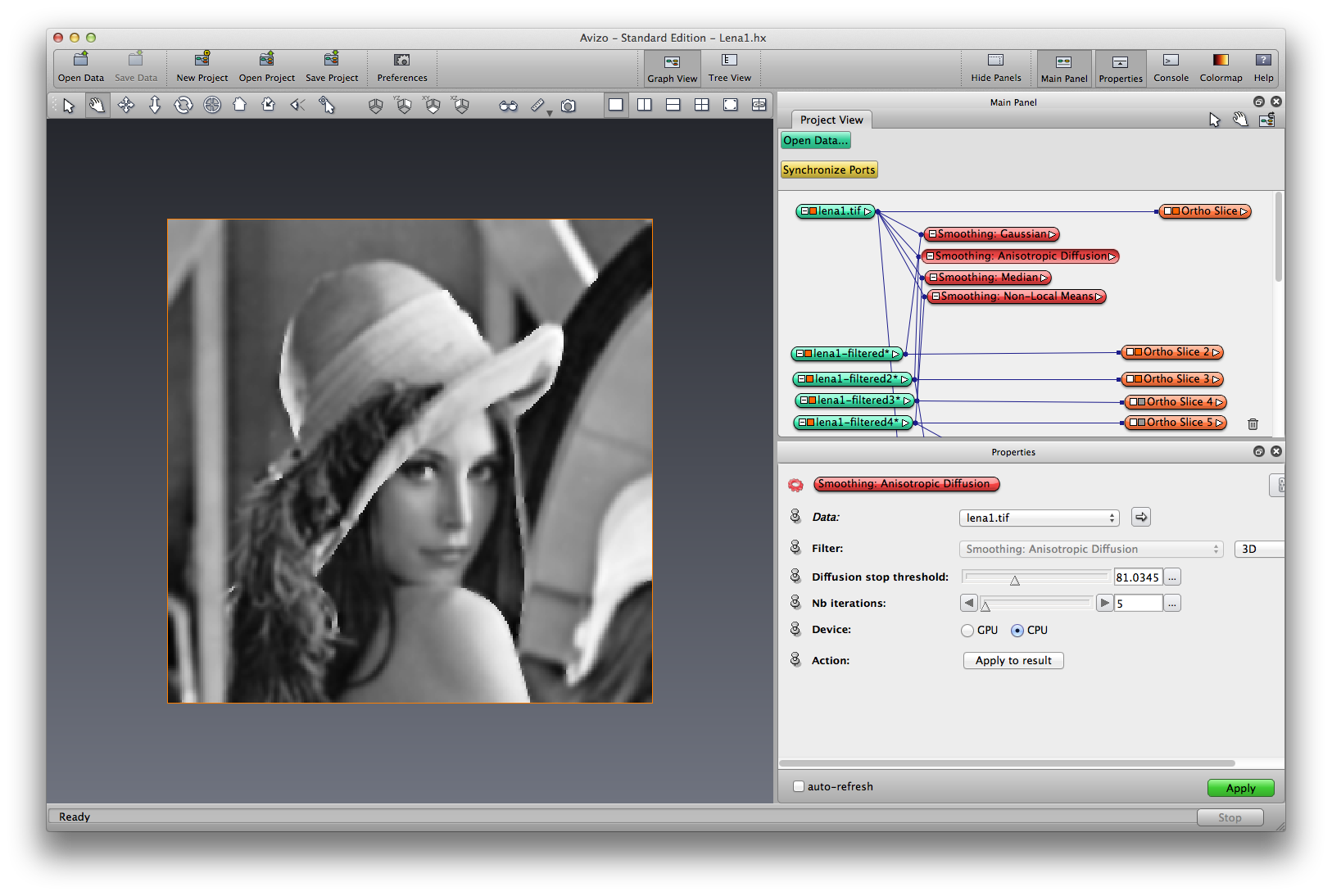
7. Right click on lena, choose Image Filters->Smoothing:Median, apply, a filtered image object is created, rename it lena-median. The median filter considers each pixel in the image in turn and looks at its nearby neighbors. It replaces its pixel value with the median of the neighboring values.

   

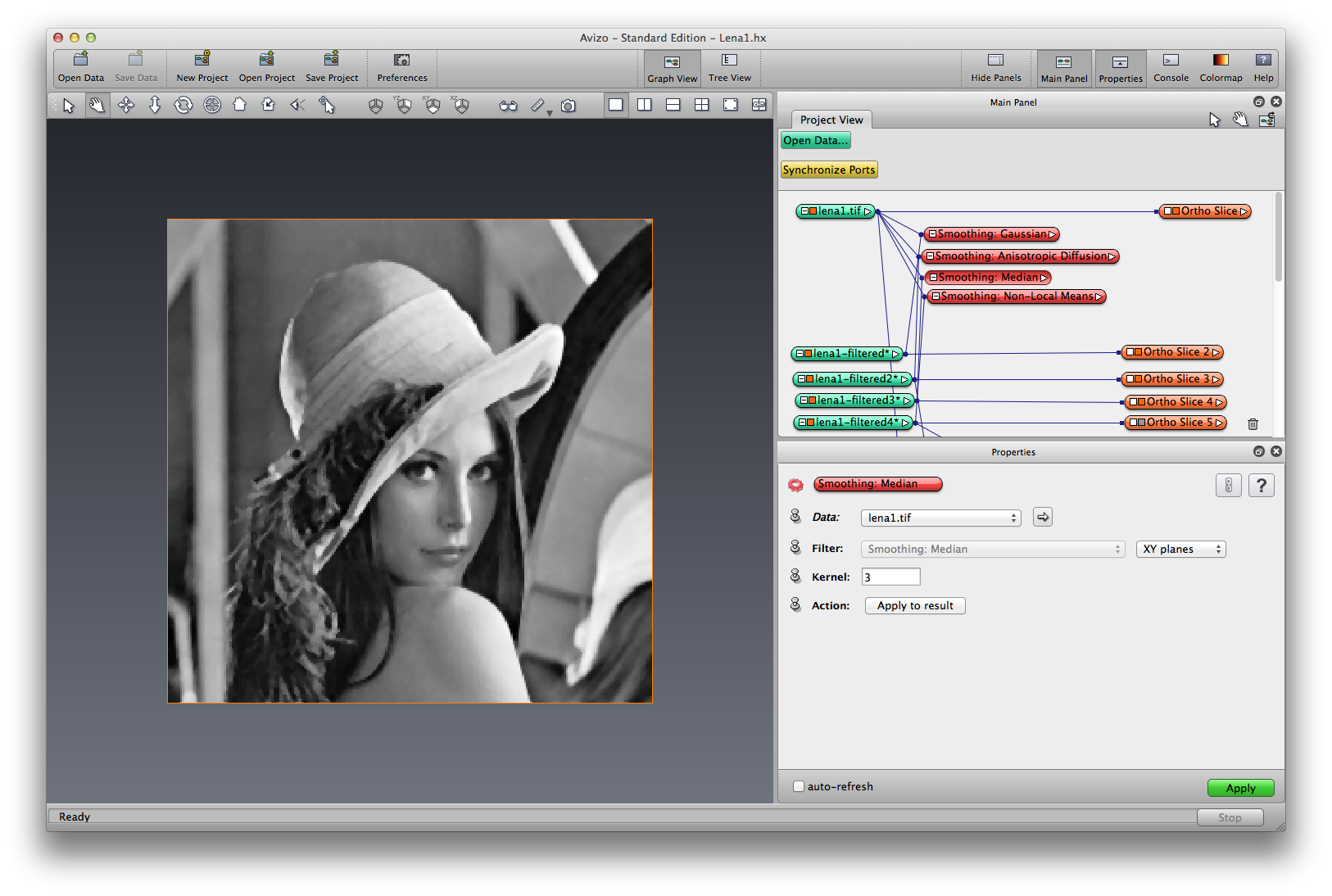
8. Right click on lena, choose Image Filters->Smoothing:Non-Local Means, apply, a filtered image object is created, rename it lena-nonLocalMeans. Non-Local Means smoothing uses an adaptive convolution kernel, the amount of weighting for a pixel is based on the degree of similarity between a small patch centered around that pixel and the small patch centered around the pixel being de-noised.

   

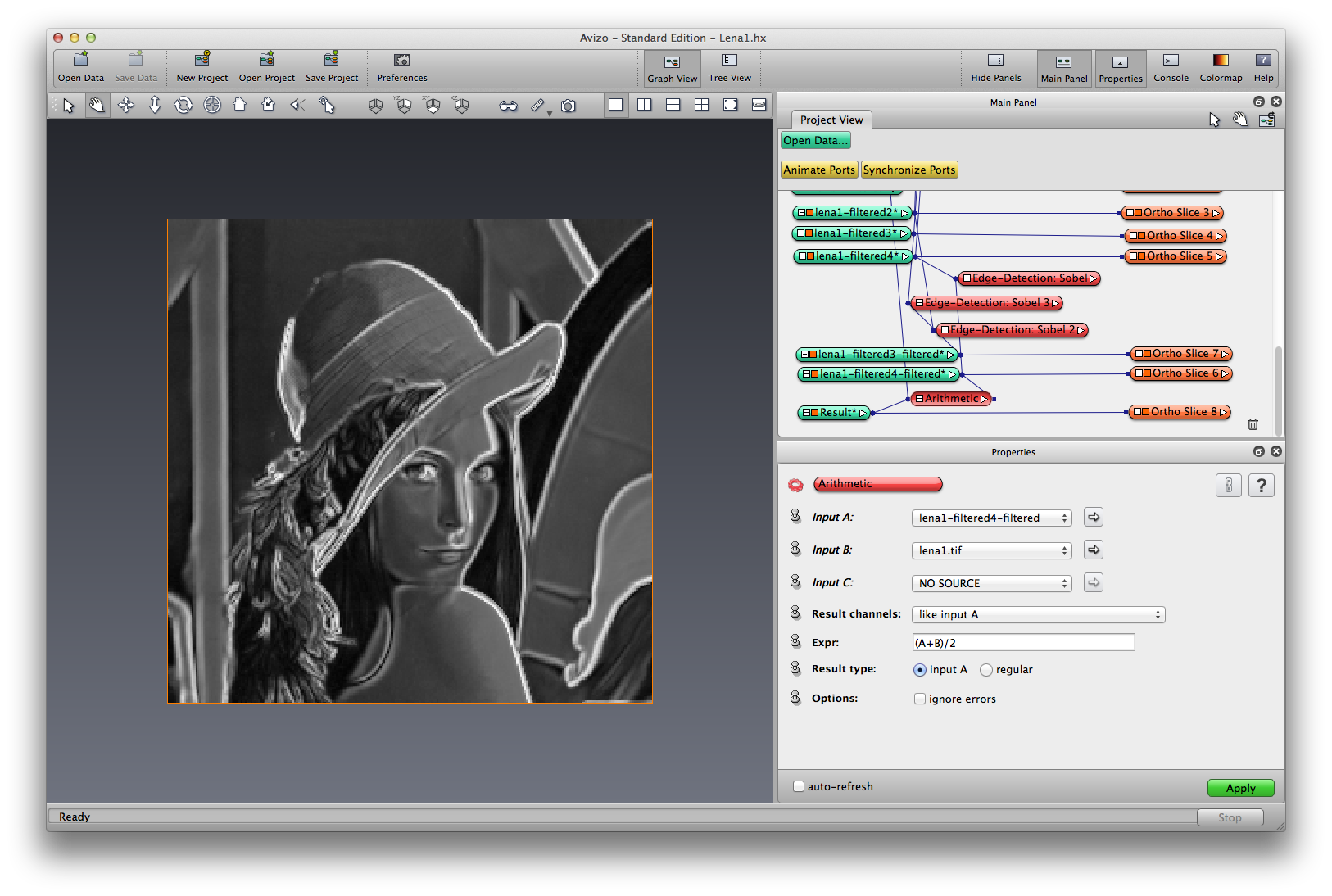
9. Right click on lena-median, choose Image Filters->Edge-Detection:Sobel; Do the same to lena-nonLocalMeans, rename the result lena-nonLocalMeans-sobel. Because the Non-Local Means smoothing does a better job reserve image features such as edge, the result of edge-detection is better.

   

10. Right click on lena-nonLocalMeans-sobel, choose compute->Arithmetic, set input A to lena-nonLocalMeans-sobel, input B to lena, input C to: NO SOURCE, Result channels to: like input A, Expr to : (A+B)/2, Result type to: input A, apply. A combined image of original lena and edge detected lena is produces. Use orthoslice to visualize.